Sorry, dieses HTML-Dokument ist aufgrund der
fehlerhaften docà html-Konvertierung von Microsoft nicht perfekt
formatiert.
Inhaltsverzeichnis
1 Das Software-Tool
"Data-Stream-Network" *
1.1 Idee des "Data-Stream-Networks" *1.2 Bedienung und
Oberfläche *
1.3 Implementierung *
1.3.1 C++ *
1.3.2 Tcl/Tk *
1.3.3 Interne Module des Programms *
1.3.4 Interne Programmstruktur *
1.4 Integrierte Algorithmen und technische
Eigenschaften *
1.5 Erweiterungen *
1.6 Arbeiten mit "Data-Stream-Network"
*
2 Literaturverzeichnis *
- Das
Software-Tool "Data-Stream-Network"
-
- Idee des
"Data-Stream-Networks"
Im Jahr 1994 entwickelte sich die Idee zu
diesem Programm aus Ergonomieüberlegungen. Es war, in Betracht
der durchzuführenden Datenanalysen, notwendig die
Arbeitsmethoden effizienter zu gestalten. Die übliche
Vorgehensweise ohne dieses Tool war folgende:
Für eine gegebene Aufgabe werden (i.a. viele)
Algorithmen entwickelt und in einem Programm miteinander
verbunden. Das Programm ist damit nur für diese Art von
Untersuchungen verwendbar. Für kleine Variationen innerhalb der
Untersuchung muß fortwährend der Sourcecode umgeschrieben
werden. Sollen gänzlich andere Probleme gelöst werden, muß ein
komplett neues Programm entwickelt bzw. aus Algorithmen von
vorhandenem Programmcode aufgebaut werden. D.h., für jede neue
Aufgabe oder sogar Variation der Aufgabe ist ein eigenständiges
Programm notwendig. Der Grund für die Spezialisierung der
Programme liegt dabei meistens nicht in den verwendeten
Algorithmen, die sich in vielen Fällen kompatibel erstellen
lassen, sondern in deren Auswahl, Varianten, Reihenfolge
und Verknüpfung.
Ein Ausweg aus diesem Problem wäre die
Entwicklung eines einzigen universellen Programmes.. Um es für
alle eventuellen Anwendungen zu rüsten, müßte es allerdings
sehr komplex sein. Die mannigfaltigen Möglichkeiten der
Zeitreihenanalyse wären auf herkömmlichem Wege nur durch eine
komplizierte Struktur von Parametern einstellbar. Praktisch
ließe sich dieser Weg daher nur für eine sehr eingeschränkte
Klasse von Anwendungen realisieren.
Eine andere Möglichkeit wäre es, die
Untersuchungsschritte auf viele einzelne konfigurierbare
Programme zu verteilen, die je nach Anwendung über das
Betriebssystem miteinander verknüpft werden. Der Datenaustausch
zwischen den Modulen muß dabei über kompatible (Datei-)
Schnittstellen oder über Pipes erfolgen. Letztendlich wird
jedoch durch diese Modullierung das Problem nur vom Programmcode
auf die Betriebssystemebene verschoben: Die Verkettung der
Module, der Datenaustausch und das Setzen der Parameter müßte
entweder für jede Berechnung interaktiv erfolgen oder durch
Scriptprogrammierung wieder individuell programmiert
werden. Z. B. müßte das Aufteilen von Daten auf mehrere
Verarbeitungszweige, das Zusammenführen bzw. der Vergleich der
Ergebnisse und die Ausführung der Programme richtig
synchronisiert werden. Weiterhin müßte die Optimierung der
Verfahren und Parametereinstellungen durch viele
Programmdurchläufe (und Umprogrammierungen) erfolgen. Der
zusätzliche Arbeitsaufwand für die Verwaltung und Steuerung der
Module würde von der eigentlichen Aufgabe ablenken. Große
Untersuchungen ließen sich bei dieser Vorgehensweise nicht
professionell abwickeln.
Daher erschien es notwendig ein komfortables
und flexibles Arbeitswerkzeug für die Zeitreihen- und
Datenanalyse mit folgenden Anforderungskriterien zu entwerfen:
Das Programm sollte nach dem bewährten Modulprinzip arbeiten -
die Arbeitsabläufe werden in kleine und gut abgestimmte
wiederverwendbare Einheiten zerlegt. Dabei ist es wichtig genau
abzuwägen, wie universell oder speziell die einzelnen Module zu
entwickeln sind. Falls sie zu speziell sind, sind sie nicht
wiederverwendbar, sind sie zu primitiv müssen zu viele Module
für eine Anwendung vernetzt werden. Dieses Programm sollte alle
Module komfortabel verwalten und es ermöglichen sie schnell und
einfach anzusteuern, zu verbinden sowie die Berechnungen
automatisch ablaufen zu lassen. Die Parameter und die Art der
verwendenden Algorithmen müßte einfach zu verändern und deren
Wirkung direkt zu erhalten sein, so daß Optimierungen schnell
durchzuführen sind. Alle Standardalgorithmen der
Zeitreihenanalyse sollten schon enthalten sein und die grafische
Darstellung der Ergebnisse müßte auch schon im Programm
integriert sein. Das Programm sollte kurz gesagt in einer
abstrakten Form den Umgang mit Daten ermöglichen und den
Benutzer mit internen Details verschonen, so daß er sich ganz
auf seine Aufgabe konzentrieren kann.
Die geforderten Eigenschaften lassen sich somit
wie folgt zusammenfassen:
-
- Wiederverwendbare Module
-
- Kompatible Schnittstellen zwischen den
Modulen
-
- Einfache und übersichtliche
Vernetzung der Module
-
- Leichte Einstellung und
Optimierung der Parameter
-
- Einfache und einheitliche
Bedienung aller Module
-
- Angebot aller Standardverfahren
der Zeitreihenanalyse
-
- Integration einer grafischen
Darstellung der Ergebnisse
Einen entscheidenden Hinweis für die mögliche
Gestaltung einer Bedienungsoberfläche, mit der diese Kriterien
erfüllt werden können, gab das Softwarepaket KHOROS, das
ursprünglich von der University of New Mexico (USA) entwickelt
wurde. Mit dem Programm kann interaktiv grafisch
ein Netz der Bearbeitungsroutinen, mit denen die Daten behandelt
werden sollen, konstruiert und die Ergebnisse grafisch ausgegeben
werden. Leider war der Umfang und die Komplexität des Programmes
- die komplette Version enthält 500 MB Sourcecode - so groß,
daß es überdimensioniert für die Zielsetzung erschien.
Außerdem entsprach das Programm hinsichtlich seiner Bedienung
und Flexibilität nicht den Anforderungen.
Daher wurde ein eigenes Programm nach diesem
Vorbild ohne die Schwächen konstruiert: Mit dem entwickelten
Programm können, ähnlich wie bei KHOROS, viele Algorithmen
schnell und einfach miteinander "verschaltet" werden.
Ebenso leicht ist es, nachträglich Änderungen an der
Vernetzungsstruktur oder den Parametern durchzuführen und das
Ergebnis dieser Manipulationen zu erhalten. Die Konstruktion der
Algorithmenvernetzungen geschieht interaktiv mit Hilfe eines
grafischen Editors und läßt sich unter dem Stichwort
"Grafische Programmierung" einordnen. Die gesamte
Algorithmusstruktur wird aus kleinen, überschaubaren Einheiten
aufgebaut. Diese so erzeugte Netzwerkstruktur ist als ein
Filtersystem zu verstehen, in das auf der Eingabeseite ein oder
mehrere Datensätze einfließen, mit verschiedenen Algorithmen
bearbeitet werden und an der Ausgabeseite i.a. auch grafisch
aufbereitet ausgegeben werden. Aus diesem Bild ist der Name
"Data-Stream-Network" entstanden.
-
- Bedienung
und Oberfläche
- Das Data-Stream-Network-Programm
(DSN) läßt sich sehr leicht auf einem
MS-Windows-Rechner installieren. Das komprimierte
Programmpaket paßt auf eine HD-Diskette (1.44
kB) und wird mit dem enthaltenen
Installationsprogramm auf die Festplatte kopiert
und entpackt. Außerdem müssen zwei Public
Domain Programme auf dem Computer installiert
sein: GNUPLOT zur grafischen Datenrepräsentation
und die Scriptsprache Tcl/Tk der Firma SUN, mit
der die grafische Bedienungsoberfläche
programmiert wurde.
Das
DSN präsentiert sich beim Start als eine
Arbeitsfläche, auf der das Netz der Algorithmen
konstruiert wird (Abbildung 1). Die Fläche
zum Aufbau der Struktur ist nicht durch die
Bildschirmgröße beschränkt. Durch Scrollbars
können andere Bereiche des großen virtuellen
Desktop sichtbar gemacht werden. An den Seiten
ist der Desktop mit verschiedenen aktiven Widgets
zur Steuerung des Programms und passiven Widgets
als Statusanzeige umgeben.
Die obere Menüzeile stellt
allgemeine Kommandos zur Programmsteuerung zur
Verfügung. Shortcuts für häufig benutzte
Befehle sind am linken Fensterrand in Form von
Smart Icons angebracht. Die wichtigsten Befehle
sind selbstverständlich auch über Tastenkürzel
zu erreichen.
In der zweiten Menüzeile kann
man die eingebauten Algorithmen, nach
Bedeutungsgruppen sortiert, anwählen. Durch
einen zweiten Mausklick auf eine leere Stelle des
Desktops wird ein Algorithmus, durch eine großes
Icon dargestellt, "fallengelassen". Die
Algorithmen werden dabei als Filter aufgefaßt,
d.h. sie müssen auf der einen Seite mit Daten
gespeist werden und geben auf der anderen Seite
ihre berechneten Daten aus. Für diese Ein- und
Ausgabedaten werden kleinere Icons automatisch
eingefügt und durch Pfeile, die die
Datenflußrichtung anzeigen, mit dem Algorithmus
Icon verbunden. Hat man zwei Algorithmen (incl.
der Datenknoten) auf der Arbeitsfläche plaziert,
können sie sehr einfach miteinander vernetzt
werden: Z. B. "faßt" man mit der Maus
das Ausgabe Icon "an", schiebt es über
einen Eingabedatenknoten und läßt es
"fallen" (tag, move, and drop mit der
linken Maustaste). Die beiden Datenknoten werden
nun automatisch verschmolzen und stellen jetzt
ein und denselben Datensatz dar. Mit dieser
Methode wurden Netze mit bis zu 200
Verknüpfungen konstruiert. Die Netzwerkstruktur
läßt sich, mit allen darin enthaltenen Daten,
in ihrem aktuellen Zustand vollständig in eine
Datei sichern und wieder laden.
Alle Netzteile können
jederzeit verschoben oder in ihrer Struktur
verändert werden, indem man eine Verbindung oder
einen Knoten markiert, dann löscht und einen
anderen Algorithmus oder eine andere Vernetzung
einfügt. Einzelne Knoten lassen sich mit der
Maus gleichzeitig markieren und Gruppen können
mit einem "Fangrechteck" erfaßt
werden, so daß alle Befehle auch auf mehrere
Knoten gleichzeitig angewendet werden können.
Nachdem die gewünschte
Datenflußstruktur aufgebaut ist, reicht ein
doppelter Mausklick auf einen hinteren Knoten und
alle Berechnungen, die nötig sind, um diesen
Knoten zu bestimmen, werden gestartet. Jederzeit
können Struktur- oder Parameteränderungen
durchgeführt werden, deren Auswirkungen man
durch einen erneuten Mausklick erhalten kann.
Nach einem rekursiven Suchverfahren werden nur
die Teile neu berechnet, die nicht mehr der
aktuellen Netzwerkstruktur oder den aktuellen
Parametereinstellungen entsprechen. Der Zustand
der Datenknoten wird durch die unterschiedliche
Schattenfarbe angezeigt. Z. B. erkennt man
in Abbildung 1, daß das Netz bis zum
PCA-Trafo-Knoten (12) bzw. bis zu dessen
Rechenergebnis (13) durchgerechnet worden ist, da
diese Knoten und alle Knoten bzgl. der
Datenflußrichtung davor einen grauen Schatten
(auf dem Farbbildschirm: grün) besitzen. Die
Knoten dahinter sind noch nicht aktualisiert und
schwarz (Schatten (auf dem Farbbildschirm: blau),
falls sie Daten enthalten bzw. hellgrau, falls
sie leer sind. Die Aktualisierung der Knoten wird
durch das schrittweise Durchfärben der Schatten
während der Berechnung visualisiert.
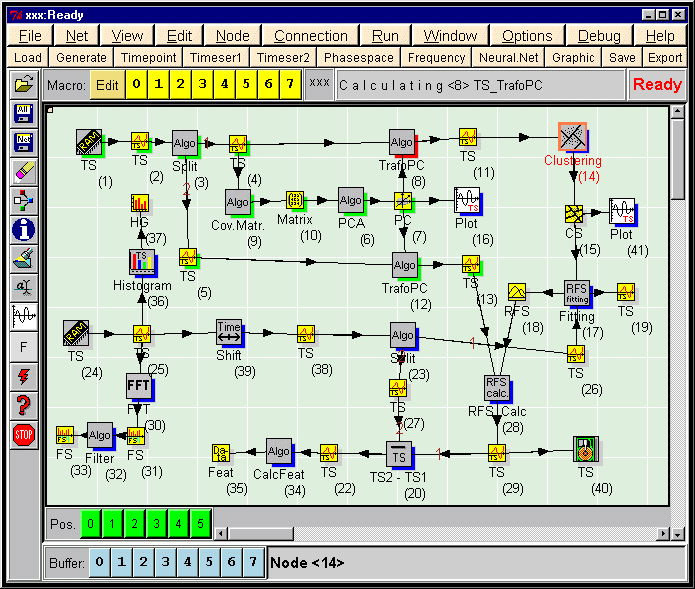
Abbildung 1: Bildschirmhardcopy des
Data-Stream-Networks mit einem kleinen
Beispielnetz:
Ein ähnliches Netz ist
für die Downscaling-Untersuchung in dieser
Arbeit verwendet worden. Hier eine allgemeine
Interpretation: Stellen wir uns vor, uns liegen
Messungen eines Observablenvektors A vor, der den
Zustand eines dynamischen Systems S zu bestimmten
Zeitpunkten beschreibt. Diese Daten stehen uns in
Form einer Zeitreihe als Datei auf der Festplatte
zur Verfügung. Sie werden durch den
Zeitreihenlade-Knoten (1) in das Netz gebracht
und liegen dort durch Knoten (2) symbolisiert zur
Weiterverarbeitung bereit. Weiterhin haben wird
Daten einer andere Observable B des Systems, die
über einen unbekannten inneren
Zusammenhang mit dem Zustand des Systems
verknüpft ist (24). Wir stellen uns jetzt die
Aufgabe, aus den zwischen den beiden Datensätzen
bestehenden Korrelationen die Abbildung vom
ersten Observablenvektor auf die zweite
Observable zu schätzen. Da wir eine
allgemeingültige Abbildung suchen und nicht nur
die vorliegenden Datensätze approximieren wollen
(Stichwort: Overfitting), teilen wir unsere Daten
in Trainings- und Testdatensatz auf. Mit Knoten
(3) für A und Knoten (23) für B wird diese
Aufgabe erledigt. B sei eine multivariante
Zeitreihe mit 100 Observablen pro Zeitpunkt, die
stark untereinander korreliert sind. Um das
Rauschen herauszufiltern und um die Algorithmen
nicht mit unnötigen Datenmengen zu belasten,
werden die Daten vorverarbeitet. Dazu bestimmen
wir die Kreuzkorrelationsmatrix (10) mit (9) und
wenden eine Hauptkomponentenanalyse (PCA) in (6)
an. Das Ergebnis liegt in (7) vor und wird mit
(16) in eine Grafik gedruckt und interpretiert.
Wir erkennen, daß nur die ersten 5 Komponenten
relevante Information enthalten und stellen
dieses in der PCA-Transformation (8) ein.
Derselbe Parameter wird in (12) für den
Testdatensatz (5) verwendet. Die Menge der
reduzierten jetzt 5-dimensionalen Datenpunkte
(11) wird in (14) einer Phasenraumclusterung
unterzogen und liefert in (15) die Vorstufe eines
neuronalen Netzes (RBFS). Das Netz wird in (17)
mit den Trainingsdaten (26) gefittet und liefert
in (18) das RBFS als Ergebnis. Dieses wird mit
(28) auf den Testdatensatz (13) angewendet. Die
berechnete Zeitreihe (29) sollte jetzt ähnlich
der gemessenen Zeitreihe (27) sein. Um dieses zu
prüfen, werden sie voneinander abgezogen (20).
Die Differenzzeitreihe (22) wird dann auf ihre
Kenngrößen, wie z.B. die Streuung, untersucht.
Der Inhalt der Datenknoten
(Daten) und der Algorithmusknoten (Parameter)
kann durch einen Befehl (Shortcut: rechte
Maustaste) sichtbar gemacht und verändert
werden. Es öffnet sich eine Dialogbox, in der
der Knoteninhalt in einem ASCII-Format
dargestellt ist. Alle Datenknoten besitzen
zusätzlich eine grafische Darstellung. Durch
einen speziellen Befehl wird der Inhalt des
gerade markierten Knotens aufbereitet und an das
externe Programm GNUPLOT geleitet. Jeder Datentyp
(z.B. Zeitreihe, Frequenzspektrum) besitzt
eine standardisierte Darstellungsform, die in
diesem Fall benutzt wird. Sollen speziellere
Grafiken erzeugt werden, ist für jeden Datentyp
ein Plotalgorithmus entwickelt worden, durch
dessen Parameter die Darstellung genau angepaßt
werden kann. Die Einstellungen beziehen sich
dabei auf Stile wie Farben, Linienarten,
Beschriftungen, Achsenabschnitte etc. und
generelle datenabhängige Formate, z.B. wie die
Kanäle einer multivarianten Zeitreihe auf die
verschiedenen Koordinatenachsen verteilt werden
sollen (Phasenraumplot). Die Plotalgorithmen
erzeugen für einige Datentypen auch
3-dimensionale Grafiken. Dabei ist die
Darstellung der Clusterung eines 3-dimensionalen
Attraktors (Abbildung 2) sehr eindrucksvoll.
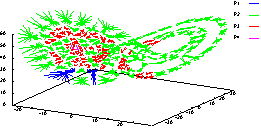
Abbildung
2: Clusterung des
Lorenz-Attraktors (5000 Beispielpunkte). Die
Graustufe gibt die Tiefe im binären Teilungsbaum
an: In Gebieten (P4, P3) mit höherer Punktdichte wird
häufiger geteilt.
Die Bedienung des Programmes
ist durch das natürliche und einfache Prinzip
schnell zu erlernen. Die Dokumentation des
Programmes ist zum größten Teil in die
Oberfläche integriert: Die Bedeutung der
einzelnen Knöpfe und Felder wird in einer
Textzeile am unteren Fensterrand eingeblendet,
wenn das entsprechende Objekt selektiert ist oder
wenn die Maus "darauf zeigt". Die Hilfe
für die einzelnen Algorithmen und Datentypen
läßt sich direkt von der Dialogbox zum
Editieren der Knoten einblenden: Es erscheint ein
Text, der die Bedeutung und die
Einstellungsmöglichkeiten des Knotentyps
erklärt.
Mit dem DSN können Analysen
schnell und komfortabel durchgeführt werden.
Verschiedene Netzvarianten lassen sich einfach
konstruieren, Parametereinstellungen können
schnell variiert werden. Das Resultat dieser
Veränderungen ist immer nur ein Mausklick (und
Rechenzeit) entfernt.
Für einige Anwendungen war
jedoch die Bedienung per Hand nicht ausreichend.
Immer wiederkehrende systematische
Arbeitsschritte, die z.B. bei der Feinjustierung
von Parametern oder der Untersuchung von vielen
gleichartigen Datensätzen anfallen, sollten
automatisiert werden. Eine erste Idee bestand
darin, den Netzwerkeditor um Schleifen, logische
Verzweigungsstrukturen und automatische
Parametereinstellungen zu erweitern. Bei näherer
Überlegung stellte sich jedoch heraus, daß
dieser Weg einen unverhältnismäßig großen
Programmieraufwand erfordert, wenn diese
Möglichkeit in einer allgemeinen Form in
die Netzwerkstrukturen eingebaut werden soll. Die
Flexibilität, die nötig ist, um den
Programmablauf der mannigfaltigen
Anwendungsmöglichkeiten zu steuern, ist dabei
nur schwer zu erreichen. Deshalb wurde ein
anderer Weg eingeschlagen: Das
Data-Stream-Network wurde um eine Scriptsprache
ergänzt. Diese Erweiterung basiert auf der
Scriptsprache Tool Command Language (Tcl), auf
die im Kapitel 2.3.2 eingegangen wird. Tcl eignet
sich aufgrund seiner guten Stringverarbeitung
hervorragend für diese Aufgabe. Tcl läßt sich
auch um eigene Befehle erweitern, die es
ermöglichen, das DSN zu manipulieren. Mit diesen
neuen Befehlen können z.B. Parameter verändert,
Knoten aktualisiert und kopiert sowie Daten
ausgelesen, verglichen und gespeichert und damit
Ergebnisse automatisch gesammelt werden. Da Tcl
alle Konstrukte höherer Programmiersprachen zu
Verfügung stellt, sind auch komplexe Steuerungen
des Netzwerkes möglich. Das DSN kann verschiede
Tcl-Scripte, hier Makros genannt, verwalten.
Jedes Makro wird durch einen Button am
Fensterrand dargestellt und ermöglicht somit,
beliebige komplexe Abläufe schnell anzusteuern.
Im Anhang wird die Bedienung
des Data-Stream-Networks an praktischen
Anwendungsbeispielen demonstriert. Man erhält
darin auch einen Überblick über die wichtigsten
Algorithmen im Programm.
- Implementierung
-
- C++
- Das Gerüst des
Data-Stream-Networks wurde komplett in
C++ programmiert. Alle selbst
entwickelten Algorithmen und alle aus
fremden C-Bibliotheken entnommenen
Algorithmen wurden in eigenständige
C++-Klassen eingebunden. Der
objektorientierte Ansatz dieser
Programmiersprache erfordert eine gewisse
Zeit des Umdenkens. C++ besitzt eine hohe
Abstraktionsebene und ermöglicht bessere
Kapselung von Daten und
Prozeduren. Auch wird die Vererbung zur
Verfügung gestellt, wodurch in
hierarchischer Struktur und somit
übersichtlich programmiert werden kann.
C++ kann so erweitert werden, daß eine
an ein spezielles Problem angepaßte
Programmiersprache entsteht. In dem
Programmpaket DSN wurde intensiv von
dieser Möglichkeit Gebrauch gemacht.
Der Hauptgrund für die Wahl von
C++ ist aber deren allgemeine
Verfügbarkeit und Standardisierung,
wodurch die Entwicklung einer Software,
die auf verschiedenen Betriebssystemen
läuft, ermöglicht wird. Ein weiterer
Vorteil ist die Verfügbarkeit von
umfangreichen Bibliotheken von
Algorithmen und Tools in C bzw. C++.
- Tcl/Tk
- Die Tool Command Language
(Tcl) ist eine sehr leistungsfähige
Interpretersprache, die von Prof. John
Ousterhout an der University of
California at Berkeley ab 1988 entwickelt
wurde. Der Kern dieser Sprache ist die
String- und Listenverarbeitung. Alle
Variablentypen sind letztendlich Strings,
die entsprechend interpretiert werden
(z.B. als float oder int). Auch
Programmcode kann in Variablen abgelegt
und interpretiert werden, so daß ein
laufendes Programm um neuen Code
erweitert werden kann. Diese Möglichkeit
wird bei der Programmierung der Makros im
DSN eingesetzt. (Weitere Informationen zu
Tcl in [3] und [4])
Die
wichtigste Erweiterung von Tcl ist das
Tool Kit (Tk), das den entscheidenden
Ausschlag für die Verwendung dieser
Sprache gab. Durch das Tk wird der
Tcl-Interpreter um umfangreiche Befehle
zur grafischen Oberflächenprogrammierung
erweitert. Mit sehr einfach aufgebautem
Programmcode lassen sich Fenster mit
vielen verschiedenen Arten von Widgets
erzeugen und damit interaktive
Dialogboxen aufbauen. Durch die
Kombination von Tcl und Tk ist es
möglich, vollständige interaktive
Anwendungen zu erstellen ohne andere
Programmiersprachen zu verwenden.
Tcl/Tk ist jedoch nicht
für alle Anwendungen geeignet. Numerisch
intensive Algorithmen laufen in
compilierbaren Sprachen schneller. Tcl/Tk
bietet daher die Möglichkeit, sich mit
verschiedenen anderen Sprachen (C,
Pascal, FORTRAN) zu verbinden. Es ist
möglich, von C aus alle Tcl/Tk-Befehle
aufzurufen und umgekehrt von Tcl/Tk aus
auf Prozeduren und Variablen des
C-Programmes zuzugreifen. Dieses
ermöglicht letztendlich die Steuerung
eines C-Programmes durch die
Benutzeraktionen (Maus, Tastatur), die
von Tk registriert werden.
Tcl ist schnell zu
erlernen und verkürzt durch seine
Struktur auch die Entwicklungszeit. Es
stellt Möglichkeiten zur Verfügung, die
in C++ nur durch aufwendige
Programmierung erreicht werden können.
Dazu gehören z.B. die interaktiv
skalierbaren Dialogboxen und die
Steuerung der Oberfläche durch eine sehr
flexible Bindung an verschiedenartigste
Benutzeraktionen. Beeindruckend sind auch
die Möglichkeiten, die sich durch das
canvas-widget eröffnen: Grafische
Elemente können als Objekte auf
dem canvas plaziert, verschoben und
skaliert werden. Die Verwaltung und
Restaurierung des Bildschirmhintergrundes
und die Überlappung der Objekte
(z-Koordinate) wird selbständig von Tk
verwaltet.
Tcl/Tk entlastet durch
seine abstrakte Form von
systemspezifischer Programmierung und ist
dadurch auch kompatibel. Da es
Tcl/Tk-Pakete für alle wichtigen
Betriebssysteme (X-Windows-UNIX,
MS-Windows, OS/2, Macintosh) gibt, trägt
es dazu bei, das "babylonische
Sprachengewirr" unter den Systemen
zu umgehen.
Ein weiteres
herausragendes Merkmal dieses
Programmiersystems ist die eingebaute
Option, die Sprache fundamental durch
Binärcode zu erweitern. So existieren
z.B. fertige Module, um grundsätzlich
neue Widgets zu erzeugen (TIX) und
Flächen- bzw. Liniengrafiken zu erzeugen
(BLT). Es ist geplant, diese beiden
leistungsfähigen Erweiterungen in die
nächste Version des DSN zu integrieren.
- Interne
Module des Programms
Auf die C++-Programmierung an sich kann hier
nicht eingegangen werden. Es wird auf die Literatur [3] und [6] verwiesen.
In C++ kann nicht immer zwischen Daten- und
Prozedurstrukturen unterschieden werden: Klassen können
gleichzeitig Daten und Prozeduren enthalten. Trotzdem hat man
eine anschauliche Vorstellung von der Funktion einer Klasse und
teilt sie nach ihrem Gebrauch in Daten und Prozeduren ein. So
würde man z.B. Punkte, Farben, Zeitreihen, Fourierspektren etc.
zu den Daten und die Algorithmen, die mit diesen Daten arbeiten,
zu den Prozeduren rechnen.
Die Algorithmen im DSN sind aber erweitert
programmiert worden: Sie enthalten auch Daten - nämlich ihre
Parameter. Die Einbettung der Parameter in die Algorithmen hat
den Vorteil, daß vor dem Start der Berechnungen nicht alle
Parameter (es sind teilweise bis zu 30) mit angegeben werden
müssen. Sie werden durch den Constructor auf Standardwerte
gesetzt, die jedoch einzeln verändert werden können. Außerdem
liegt alles, was die Berechnung definiert, ohne globalen Kontext
kompakt in einer Klasse vor und ermöglicht so eine einheitliche
Behandlung von Daten und Prozeduren, was für die interne
Verwaltung des DS-Netzes notwendig ist (siehe später).
Diese Art der Programmierung ist eng mit einer
anderen Problemlösung verknüpft. Zu Beginn der Arbeit am DSN
trat immer wieder das gleiche Problem auf: Daten mußten in eine
Datei gespeichert und geladen, Parameter eingestellt und die
Ergebnisse angeschaut und beurteilt werden. Immer wieder mußte
ähnlicher Code für die vielen verschiedenen Datentypen neu
programmiert werden, um den im Prinzip immer gleichen Vorgang zu
ermöglichen: Die Transformation von binär nach ASCII und
umgekehrt. Die Lösung besteht darin, eine Containerklasse zu
programmieren, die generell den Umgang mit Daten wesentlich
vereinfacht: Auf dieser entwickelten Klasse VarList, als Abkürzung
für "Variablenliste", beruhen alle im DSN verwendeten
Datenstrukturen. Als Children von VarList erben sie deren
Fähigkeiten, welche sind:
-
- Standardisiertes Speichern von Daten
-
- Laden von Daten in einem
Standardformat
-
- Menschenlesbare Darstellung der
Daten (ASCII)
-
- Editieren der Daten
-
- Fehlertolerante Interpretation
-
- Verwalten von mehreren
Datenlisten in einer Datei
Mit der geerbten Elementfunktion "AddVar" registriert man eine Variable in einer Instanz von VarList. z.B.:
int fifo, WindowSize;
Vector<float> filter;AddVar("Filterform",fifo,0);
// 0-Rechteckfilter, 1-Spez. Filter
AddVar("WindowSize",winsize,10);
// Filtergroesse
AddVar("Filter",filter);
// Ist Vektor
filter.SetStr("1
2 3.5 2 1"); // Möglichkeit einen Vektor mit
// einen String
Standardwerte zu setzen
Der erste Parameter der AddVar-Funktion gibt
Namen der Variablen in der ASCII-Darstellung, der zweite die
C-Variable, von der die Adresse und der Typ in VarList
gespeichert wird. Diese beiden Angaben ermöglichen, daß die VarList-Klasse
intern auf die Variable zugreifen kann. Im dritten Parameter
stehen die Defaultwerte. VarList unterstützt dabei alle Standardvariablentypen (char, int, float, double) und die definierten Typen (Boolean, String, Vector, Matrix, Color,
Intervall etc.).
Durch die Anwendung dieser einen Prozedur sind
alle obigen 6 Punkte für die jeweilige Variable in einem Schritt
erledigt. Wenn eine Instanz der VarList-Klasse z.B. mit
Namen "MovingAverage" definiert wird, sieht die durch VarList zu
Verfügung gestellte ASCII-Darstellung der Daten folgendermaßen
aus:
[MovingAverage]FilterForm = 0
WindowSize = 10
Filter = 1 2 3 2 1
[END] of
[MovingAverage]
In dieser Darstellung wird auch der Datentyp
gespeichert, geladen und editiert. Gerade das Speichern in und
das Lesen aus einer Datei wird durch diese aufwendige aber
übersichtliche Darstellungsform fehlertolerant gehalten. In der
üblichen Programmierung müßten für jeden Datentyp
Speicherprozeduren und dazu kompatible
Ladeprozeduren programmiert werden (doppelte Arbeit). Dabei
müßte exakt in derselben Art und Reihenfolge geschrieben wie
gelesen werden. Falls die Datenstruktur im Laufe der Datenanalyse
und der Programmweiterentwicklung geändert würde, könnten alte
Dateien nicht mehr gelesen werden und erzeugten
Programmabstürze. VarList ist fehlertolerant und funktioniert immer - neue
Variablen werden auf Defaultwerte gesetzt, falsche Variablennamen
werden ignoriert. Desweiteren können verschiedene
Variablenlisten in einer Datei verwaltet und über ihren Namen
unterschieden werden.
Die folgenden Zeilen zeigen den vollständigen
Code für die Definition einer Childclass. Sie verdeutlichen, wie
kurz und einfach eine Datenverwaltung mit der VarList-Klasse
programmiert werden kann:
class MovingAverage:
public VarList { int fifo;
int winsize;
vector<float>
filter;
MovingAverage() //
Constructor
{
AddVar("Filterform",fifo,0);
AddVar("WindowSize",winsize,10);AddVar("Filter",filter);
filter.SetStr("1 2 3.2 1");
}
}
Durch die Abstammung von VarList hat MovingAverage
folgende Routinen geerbt:
| Load(String FileName) |
Laden der
Variablen |
| Save(String FileName) |
Speichern der
Variablen |
| GetStr() |
ASCII-Darstellung
der Variablen |
| SetStr(String s) |
Interpretiert
Strings |
| Edit() |
Verändern
mit einem Editor |
| FindeSection(ifstrem*,SectonName) |
Findet VarList-Name
in einer Datei
(Beginn einer Datensektion: [Name]) |
| ~VarList() |
Destructor |
Auch komplexere Datentypen, wie z.B.
Zeitreihen, beruhen auf der VarList-Klasse. Um die
zusätzlich in der Klasse enthaltenen Daten abzuspeichern,
müssen die Elementfunktionen GetStr, SetStr, Load und
Save überschieben werden:
class Timeser: public
VarList{public:
MyStr History;
MyStr DateTime;
int ChannelSize; //
Anzahl der Datenkanäle
TimePoints Time; //
Klasse, die die Zeitpunkte verwaltet
MyStr ValueUnit; //
Einheit der Zeit (sec,day,year etc.)
Matrix<float>
Channel; // Datenwerte der multivar. Zeitreihe
...
Timeser(); //
Constructor
void Empty(); //
Deallokiert den verwendeten dynamischen Speicher
~Timeser();......//
Destructor
...
int Load(String
FileName); // Lädt die Zeitreihe
int Load(String
FileName); // Speichert die Zeitreihe
...
} ;
Ein Algorithmus unterscheidet sich von einem
"einfachen" Datentyp durch die Erweiterung um die
Elementfunktion Run(..,..,..) mit der die Berechnung durchgeführt wird. Ein
Hauptprogramm, z.B. um den MovingAverage (MA) einer Zeitreihe zu bestimmen, sieht damit
folgendermaßen aus:
#include
"timeser.h"#include "ts_algor_1.h"
int main()
{ Timeser InputTS,
OutputTS; // 2 Zeitreihen anlegen
MovingAverage MA; //
MA-Algo. incl. Parameter anlegen
MA.Window=2;
MA.FilterMethode=0; // Parameter zum MA setzen
MA.Save("MovAv.par");
// Parameter speichern
InputTS.Load("test.ts");
// Zeitreihe laden
int
Error=MA.Run(OutputTS,InputTS);// MA berechnen
if(Error)
return(Error);
OutputTS.Save("test_ma.ts");
// Ergebnis speichern
return(0);
}
Alle Algorithmen haben von außen betrachtet
dieselbe Struktur und stellen dieselben Basisfunktionalitäten
zur Verfügung. Dadurch ist es möglich, sie in ein allgemeines
Verwaltungs- und Vernetzungssystem einzubinden, wie es im DSN
erfolgt ist. Mehr dazu im nächsten Abschnitt.
-
- Interne
Programmstruktur
Das komplette Softwarepaket enthält ca. 25.000
Quellcodezeilen mit über 1.000.000 Zeichen (zum Vergleich: diese
Dissertation enthält ca. 200.000 Zeichen). Um dieses
umfangreiche Projekt übersichtlich zu halten, wurde großer Wert
auf die strukturierte Programmierung gelegt. Die Möglichkeiten
von C++ unterstützen dabei diese Bemühungen.
Der Quelltext wurde auf 34 C++-Module (jedes
enthält wieder viele Klassen) und 14 Tcl/Tk-Files aufgeteilt.
Bei der Strukturierung wurde versucht die Abhängigkeiten der
Module möglichst hierarchisch oder sogar "linear" zu
halten. Es gibt wenige "parallele" Programmteile und
keine zyklischen Abhängigkeiten. Mit C++ ließen sich zwar
komplexe Abhängigkeitsstrukturen verarbeiten, dieses hätte aber
den Nachteil, daß sehr viele Module neu übersetzt werden
müßten, wenn nur ein Modul verändert wird. Durch den Aufbau
der Module wird dieses vermieden sowie das logische Verständnis
des Programmablaufes und die Fehlersuche vereinfacht.
Zu der Hierarchisierung gehört auch die
Trennung von Algorithmen (unter Schicht) und Oberfläche (obere
Schicht). Alle Algorithmen können getrennt von der DSN-Struktur
verwendet werden. Dies ist möglich, obwohl die Algorithmen beim
Einbau in das DSN auf Oberflächenelemente zugreifen und sie
manipulieren (z.B. wird der Fortschritt jedes Algorithmus in
Prozent ausgegeben). Um dieses zu erreichen, wird mit
Funktionenpointern gearbeitet, die in den unteren
Hierarchieschichten auf NULL zeigen und in den höheren Schichten auf die
entsprechende Tcl/Tk-Routine gesetzt werden.
Eine ähnlicher Hierarchieaufbau und deren
Bruch ist bei dem Programmteil zur Verwaltung des Netzwerkes
angewendet worden. Allerdings liegt hier eine Hierarchie von
Klassen in folgender Reihenfolge vor: Die Basisklasse DSNStructure
beinhaltet die Netzwerkstruktur sowie deren File-I/O. DSNAlgor stellt
die Schnittstelle zu den Algorithmen und Daten zur Verfügung,
kann Knoteninhalte konstruieren, löschen, speichern und laden
und Berechnungen durchführen (Run durchs Netzwerk). DSNManipulation
erweitert den statischen Teil des Netzwerkes durch konstruktive
Methoden: Einfügen und Löschen von Knoten und Verbindungen.
Durch DSNGraph wird die Sichtbarkeit des Netzwerkes und dessen
Animation zu Verfügung gestellt. Es enthält die Aktion des
Netzwerkes an die Oberfläche durch die Tcl/Tk-Schnittstelle.
Durch das Zwischenmodul DSNCommand werden Reaktionen auf die Benutzeraktionen bearbeitet. DSNWindows
letztendlich, die oberste Klasse, ist die Schnittstelle zwischen
den Oberflächenvents (von Tk geliefert) und dem Netzwerk. Diese
Klassenhierarchie zur Netzwerkverwaltung macht ca. 20% des
gesamten Codes des DSN aus.
DSNStructure kann auch für sich allein bestehen. Es wäre z.B.
möglich, ein Netz zu konstruieren und dieses ohne Oberfläche im
Batchbetrieb innerhalb DSNStructure laufen zu lassen. Es könnte daher als nicht sichtbares
Subnetz (komplexer Algorithmus) dienen, das als eine
Funktionseinheit in ein anderes Netz eingebettet wird. In diesem
Fall werden die Funktionen, die auf die Oberfläche zugreifen
nicht aktiviert. Dieses wird dadurch erreicht, daß diese
Funktionen im DSNStructure als virtuelle Funktionen leer deklariert sind.
Das Überschreiben dieser Funktionen durch die Klassen in den
höheren Schichten findet in diesem Fall nicht statt.
Die Netzwerkstruktur in DSNStructure baut sich
aus vielen Nodes und Conections
auf, die jeweils als eigene Klasse
definiert sind und in Listen gespeichert werden. Die
Einzelelemente enthalten Zeiger auf die anderen im Netz
verbundenen Elemente. Im Prinzip kann mit dieser Struktur jeder
Graph aufgebaut werden. Die Klasse DSNManipulation
überprüft aber jede Benutzeraktion und verhindert, daß bzgl.
des Datenflusses keine unsinnigen Netze konstruiert, sondern nur
Inputknoten mit Outputknoten sowie nur kompatible Datentypen
verknüpft werden und gibt in diesem Fall eine Fehlermeldung aus
und ignoriert die Aktion.
Jeder Knoten enthält eine int-Variable,
die die ID des Knotentyps angibt und einen void-Pointer, der
entsprechend der ID interpretiert wird (type-casting). Da alle
Knoten dieselben Basisfunktionen enthalten (durch VarList
definiert), kann durch ein identisches C-Makro auf alle Knoten
über ein CASE-Label nach ID selektiert zugegriffen werden.
-
- Integrierte
Algorithmen und technische Eigenschaften
Algorithmen und Verfahren
Die meisten Algorithmen arbeiten auch mit
multivarianten Zeitreihen.
- Generierung von mathematischen
Standardzeitreihen und Funktionen
- Normal- und gleichverteiltes Rauschen
- Logistische Abbildung, Hénon-Abbildung,
Lorenz-System, Standard Abbildung
- Autoregressiver Moving-Average-Prozeß
- Treppen-, Sinus-, Cosinus-,
Polynomfunktion
- Mathematisches Pendel
- Erzeugung und Verarbeitung von binären
Zeitreihen und Zeitpunkten
- Selektion von Zeitpunkten nach
verschiedenen Kriterien:
Schnittpunkte zweier Zeitreihen (aufwärts und abwärts
Kreuzungen getrennt bestimmt), Schwellwerte, Extrema
- Invertieren von binären Zeitreihen
- Boolean‘sche Operatoren von zwei
binären Zeitreihen (0 « 1)
- Vergleich zweier binärer Zeitreihen
Es wird die Statistik der Treffer und der Fehler
bestimmt.
- Ausschneiden von Abschnitten einer
Zeitreihe zu definierten (woanders berechnenten)
Zeitpunkten
- Optimalen Schwellwert finden
Eine kontinuierliche Zeitreihe soll durch eine
Schwellwertbildung binärisiert werden. Dieser
Algorithmus bestimmt den optimalen Schwellwert, so daß
das Ergebnis am besten mit einer zweiten gegebenen
binären Zeitreihe übereinstimmt.
- Elementare Analyse von Zeitreihen
- Mittelwert und Varianz
- Quadratsumme (Leistung)
- Minimum und Maximum
- Bestimmung der linearen
Regressionsparameter
- Umstrukturierung von Zeitreihen
- Zeitverschiebung und Zeitumskalierung
- Zerteilen von Zeitreihen bzgl. der
Zeitkoordinate
- Ausschneiden von Abschnitten einer
Zeitreihe bzgl. der Zeitkoordinate
- Zerteilen einer Zeitreihe in gleichlange
Intervalle
Die Intervallänge muß nicht teilbar durch die
Samplingrate sein.
Dadurch wurde das Problem der Schaltjahre gelöst.
- Zwei Zeitreihen verbinden
- Eine Zeitreihe N mal aneinanderhängen
- Sortieren der Daten bzgl. Größe oder
Absolutbetrag
- Ausschneiden von einzelnen Kanälen einer
multivarianten Zeitreihe
- Kombinieren von mehreren singelvarianten
Zeitreihen zu einer multivarianten Zeitreihe
Die eventuell unterschiedlichen Zeitintervalle werden
automatisch angepaßt.
- Timedelay-Transformation (Takens)
- Elementare Manipulationen von
Zeitreihen
- Umskalierung mit Festlegung von
Mittelwert, Streuung, mittlere Quadratsumme, Minimum
und/oder Maximum
- Rundung, Logarithmierung, Exponentierung,
Potenzierung
- Addition, Subtraktion, Multiplikation und
Division mit Skalaren
- Addition, Subtraktion, Multiplikation und
Division von Zeitreihen untereinander
(auch multivariant)
- Mittelwert über die Kanäle einer
multivarianten Zeitreihe
- "Inverses Timedelay"
Eine multivariante Zeitreihe wird durch diagonale
Mittelwertbildung in eine monovariante Zeitreihe
transformiert.
- Erweiterte Manipulationen und Analysen
von Zeitreihen
- Mittelwert und Streuung kumuliert
- Moving-Averages mit einfachem, linearem,
exponentiellem Filter
Beliebige Filterkkoeffizienten sind auch explizit
definierbar.
- Gleitende Streuung
Für jeden Zeitpunkt wird die Steuung einer bestimmten
Anzahl benachbarter Datenpunkte berechnet.
- Interpolation zwischen den Daten
benachbarter Zeitpunkte, Ausdünnen einer Zeitreihe
- Differenzfilter
Gleitend werden die Werte einer Zeitreihe mit definiertem
Zeitabstand subtrahiert. Statt der direkten Werte können
auch einfache gleitende Mittelwerte voneinander
subtrahiert werden.
- Bestimmung der linearen oder polynominalen
Interpolationskoeffizienten
Für jeden Zeitpunkt werden für ein Zeitfenster die
Koeffizienten bestimmt. Sie werden als multivariante
Zeitreihe ausgegeben und von einem anderen Algorithmus
zur Extrapolation in die Zukunft (Vorhersage) benutzt.
- Korrelationen
- Autokorrelationen (maximaler Zeitshift
festlegbar)
Die Berechnung erfolgt über die FFT oder direkt.
- Korrelationen zweier Zeitreihen (maximaler
und minimaler Zeitshift festlegbar)
Die Berechnung erfolgt über die FFT oder direkt.
- Korrelationen zweier Zeitreihen über ein
gleitendes Zeitfenster
Die Veränderung der Korrelation mit der Zeit kann damit
untersucht werden.
- Korrelation vieler Zeitreihen
untereinander und Bestimmung der Kreuzkorrelationsmatrix
Durch die Anwendung des Timedelay-Algorithmus kann auch
die zeitliche Korrelation untersucht werden.
- Hauptkomponentenanalyse der
Kreuzkorrelationsmatrix
- Hautpkomponententransformation einer
multivarianten Zeitreihe
- Umsortierung der Spalten und Zeilen der
Kreuzkorrelationsmatrix
Die Sortierung erfolgt automatisch so, daß man Gruppen
die stark miteinander korreliert sind (positiv wie
negativ), gut erkennen kann.
- Umsortierung der Kanäle einer
multivarianten
-
- Statistik
- kumulative Verteilungen
- Histogramme
- Frequenzanalyse
- Direkte und inverse
Fast-Fouriertransformation für 2N Stützstellen
- Direkte und inverse Fouriertransformation
für beliebige Stützstellenanzahl
- Bandfilter
- Maximum Entropie Spektrum
- Detektieren von Peaks in einem
Frequenzspektrum
- Hauptfrequenzanalyse nach Laskar [7]
- Schreiber-Rauschfilter [8]
- Direkte und inverse diskrete
Wavelettransformation (Daubechies-Basis)
- Filter im Waveletspektrum
- Vorhersage
- Autoregressive Vorhersage
- Einfache Nächste-Nachbar-Vorhersage
- Phasenraum-Clusterung
- Radial-Basis-Funktionen-System (RBFS)
- Schätzung von Lyapunov-Exponenten und
Jacobimatrix (mit RBFS)
- Grafische Ausgabe aller Datentypen
- Matrizen
Die Größe der Matrixelemente wird durch Quadrate
dargestellt.
- Hauptkomponentenzerlegung
- Zeitreihen (auch 3d)
Es sind mannigfaltige Darstellungsformen möglich.
- Fourierspektren
- Waveletspektren
- Cluster (auch 3d)
- Radial-Basis-Funktionen
- Histogramme
- Soundausgabe von Zeitreihen als wave-Datei
Technische Eigenschaften
-
- 25.000 Zeilen / 1.000.000 Bytes selbst
entwickelter C++-Code
-
- Ca. 100 Algorithmen
-
- Bis zu 500 Knoten können in einem Netz
verwaltet werden
-
- Virtueller Bildschirm von 5000 x 5000
Pixeln
-
- Netzwerkstruktur, Daten und Desktop
können komplett gesichert werden
-
- Programm spart Arbeitsspeicher, da nur die
benötigten Daten ins RAM geladen werden
-
- Alle Datenstrukturen haben grafische
Ausgabe über GNUPLOT
-
- Hilfetext für jeden Algorithmus
-
- Bedienungshilfe in Oberfläche integriert
-
- Erweiterungen
- Geplant ist eine Erweiterung der
Dateistrukturen um ein binäres Format, um das
Laden und Speichern der Netzknoten zu
beschleunigen. Dieses soll in einer generellen
Art durch die Erweiterung von VarList geschehen.
Ein
sinnvolle aber auch arbeitsaufwendige
Vervollständigung des DSN ist der Einbau einer
eigenen grafischen Datendarstellung. Diese soll
in BLT erfolgen und würde erweiterte grafische
Darstellungsformen ermöglichen und dem
Betrachter erlauben, interaktiv die Bilder zu
manipulieren (z.B. Zoomen) oder weitere
Informationen anzufordern.
Das Programm kann auch als
Basis und übersichtliche Bedienungsplattform
für weitere Algorithmen dienen.
- Arbeiten
mit "Data-Stream-Network"
In diesem Abschnitt wird an drei
Anwendungsbeispielen der Umgang mit dem Programm und einigen
Algorithmen erklärt. Die Menübefehle sind durch folgenden
Schriftstil hervorgehoben: Menüpunkt
Beispiel 1: Sonnenfleckendaten
-
- Start
In Abhängigkeit von der Konfiguration sind nach dem
Start des Programmes 1-3 Fenster zu sehen. Das Script-
und das Debugfenster benötigen Sie jetzt noch nicht. Mit
Window/Debug bzw. Window/Script lassen sie sich entfernen (Fenster bitte nicht
mit dem Windowmanager schließen). Diese Einstellungen
sowie Fenstergröße und -position können Sie für den
nächsten Programmstart mit Options/Save Geometry speichern.
-
- Einfügen eines Algorithmus
Wählen Sie Load/Timserie. Durch ein Klicken mit der Maus auf die
Arbeitsfläche werden zwei Icons eingefügt. Das große
stellt den Zeitreihenlade-Algorithmus und das kleine die
Zeitreihe dar. Sie können die Icons mit der Maus nach
der üblichen tag-move-and-drop-Methode beliebig auf dem
Desktop anordnen.
-
- Laden einer Zeitreihe
Jeder Algorithmus besitzt Parameter, die eingestellt
werden können. Für den Zeitreihenlade-Algorithmus muß
der Dateiname angegeben werden. Klicken Sie mit der
rechen Maustaste auf das Icon und stellen Sie in der
Dialogbox den Dateinamen
"tsa/data/sunspot/sonne.ts" ein. Durch einen
Doppeklick mit der Maus auf eines der beiden Icons wird
die Datei symbolisch von der Festplatte in das kleine
Zeitreihen-Icon geladen. Sie erkennen dieses daran, daß
sich die Schattenfarben des Icons zu grün verändert.
- Löschen von Dateninhalten
Markieren sie den Datenknoten und drücken Sie auf
die Space-Taste. Die Zeitreihe wird gelöscht und der
Schatten färbt sich grau. Dieser Schritt ist
normalerweise nicht nötig. Nur wenn Sie das Netzwerk
speichern wollen und z.B. zum Transport die Dateigröße
verringern wollen ist er sinnvoll. Aktualisieren Sie den
Datenknoten wieder mit einem Doppelklick.
- Standardgrafik
Wenn Sie den Datenknoten markieren und Node/Graphics wählen, wird ein Grafikfenster mit der
Darstellung der Zeitreihe geöffnet: Sie erkennen die
periodischen Strukturen der Zeitreihe.
- Verknüpfen von Algorithmen
Sie möchten jetzt das Frequenzspektrum in der
Zeitreihe untersuchen. Fügen Sie dazu den Algorithmus Frequency/FFT ein. Schieben Sie den Input-Datenknoten (auf
der linken Seite) auf die Zeitreihe des anderen
Algorithmus. Die Datenknoten werden dadurch miteinander
verbunden.
-
- Frequenzanalyse
Wenn Sie jetzt auf auf den Ausgabeknoten der FFT
doppelklicken, wird die Berechnung gestartet. Drücken
Sie die Taste "g" als Abkürzung für Node/Graphics und das Leistungsspektrum der
Sonnenfleckenzeitreihe wird dargestellt. Für viele
Menübefehle existieren Shortcuts in Form von Buttons am
linken Fensterrand oder Tastaturkürzel. Die Bedeutung
der Buttons wird am unteren Fensterrand angezeigt, wenn
Sie mit der Maus auf den Button zeigen. Die
Tastaturkürzel sind in den Menüs zu sehen.
-
- Plotalgorithmus des Frequenzspektrums
Fügen Sie Graphics/Fourierspec. ein und verbinden Sie die beiden
Fourierspektren. Mit dem neuen Algorithmus können Sie
die grafische Darstellung des Spektrums genau an Ihre
Bedürfnisse anpassen. Durch ein Klicken mit der rechen
Maustaste auf den Plotalgorithmus wird eine Dialogbox
geöffnet in der Sie die Parameter einstellen können.
Durch den Hilfeknopf werden
Einstellungsmöglichkeiten erklärt.
Stellen Sie z.B. yLogsScale=0 und Powerplot=0 ein.
Schließen Sie die Dialogbox mit OK ab (oder Taste
Return) und doppelklicken Sie auf das Icon (oder Taste
Return) und Sie erhalten eine Grafik des Spektrums mit
Real- und Imaginärdarstellung.
- Inverse FFT
Fügen Sie Frequency/FFT^-1 ein und verbinden Sie die Spektren-Icons.
-
- Plotalgorithmus einer Zeitreihe
Sie wollen jetzt die originale Zeitreihe und die
rücktransformierte miteinander vergleichen. Fügen Sie Graphics/Timeserie ein und verbinden Sie die originale Zeitreihe
mit der Inputzeitreihe des Plotalgorithmus. Der
Plotalgorithmus arbeitet mit einer einstellbaren Anzahl
von Eingabedatenknoten. Markieren Sie ihn und wählen Sie
Node/Add
Inputdatanode (oder Taste Insert).
Der Algorithmus enthält ein zusätzliches Input-Icon,
das Sie jetzt mit der rücktransformierten Zeitreihe
verbinden sollten. Durch einen Doppelklick auf den
Plotalgorithmus werden beide Zeitreihen grafisch
ausgegeben. Sie liegen übereinander, so daß sie nur
eine Kurve erkennen. Um Sie zu unterscheiden, können Sie
im Plotalgorithmus Format=0 2 setzen, wodurch die
zweite Zeitreihe im Stil "Linien mit Punkten"
gedruckt wird. Diese Formatvariable ist ein Integerarray
aus dem die Elemente zyklisch gewählt werden. Falls mehr
Zeitreihen geplottet werden als Formate angegeben sind
wird wieder mit dem ersten Arrayelement begonnen. Fast
alle Stilformate werden zyklisch benutzt. (à
Hilfetext)
- Trennen von Verbindungen
Markieren Sie die Verbindung zwischen dem FFT^-1- und
seinem Input-Icon. Drücken Sie die Delete-Taste. Die
Verbindung wird gelöscht und der Algorithmus wieder mit
einen Input-Icon versehen.
- Bandfilter
Fügen Sie Frequency/Bandfilter ein und bauen Sie diesen Algorithmus zwischen
die erzeuge Lücke im Datenfluß ein. Falls zu wenig
Platz ist, können Sie mehre Icons gleichzeitig
verschieben, indem Sie sie mit einen Fangrechteck
markieren (linke Maustaste auf leere Stelle des Desktops
und Maus bewegen). Stellen Sie im Filter MaxFreq=0.05 und
schauen Sie sich mit Zeitreihenplotalgorithmus das
Ergebnis an.
- Speichern des Netzes
Durch File/Save
as können Sie das Netz speichern
falls es noch keinen Dateinamen hat, durch File/Save All im anderen Fall. Geben Sie bitte immer einen
Datenamen mit der Endung ".net" ein.
Beispiel 2: Phasenraumplot der
Henon-Abbildung
- Neue Datei anlegen
- Mit File/New können
Sie den Desktop vollständig leeren.
- Erzeugung der Henon-Zeitreihe
- Fügen Sie Generate/Henon ein und schauen Sie sich die Zeitreihe an. Der
Algorithmus generiert in der Standardeinstellung eine
1-dimensionale Zeitreihe.
- Timedelay
- Fügen Sie Phasespace/Timedelay ein und verbinden Sie die Zeitreihen.
Aktualisieren Sie den letzen Datenknoten und schauen Sie
sich die grafische Ausgabe an. Sie sehen zwei Zeitreihen,
die um einen Zeitschritt verschoben sind. Durch die
Parameter des Timedelay-Algorithmus können viele
Varianten der Timedelay-Methode eingestellt werden.
- Phasenraumplot
- Verbinden Sie die 2-dimensionale Zeitreihe
mit einem Zeitreihenplotalgorithmus und stellen Sie dort
ein:
| GeneralStyle |
2
|
x(t)-y(t)-Plot
(statt x(t)-Plot) |
| xTimeser |
1
|
Die Daten für die
x-Achse werden aus 1.Inputzeitreihe des
Plotalgorithmus genommen. (In diesem speziellen
Fall gibt es nur eine Inputzeitreihe) |
| yTimeser |
1
|
Daten für y-Achse
auch aus 1. Inputzeitreihe |
| xChannel |
1
|
Daten für x-Achse
aus Kanal 1 (der xTimeser) |
| yChannel |
1
|
Daten für y-Achse
aus Kanal 2 (der yTimeser) |
| Format |
1
|
Nur Punkte ohne
Verbindungslinien |
Sie erhalten die 2-dimensionale Darstellung des
Henon-Attraktor. Wenn Sie jetzt im Henongenerator z.B
Size=10000 und im Zeitreiheplot, Point=0 (nur Pixel)
einstellen, erhalten Sie eine dichte Darstellung des
Attraktors.
- Histogramme
Wählen Sie Timeser1/Histogram und verbinden Sie die Inputzeitreihe mit
der generierten Henon-Zeitreihe. Die Verteilung
der Daten können Sie durch Markierung des
Histogramms und drücken der Taste "g"
erhalten. Sie können durch die Parameter auch
Histogramme mit höherer Auflösung einstellen.
Beispiel 3: Vorhersage der
Henon-Abbildung mit einem neuronalen Netzwerk
-
- Zeitverschiebung
Sie wollen jetzt ein neuronales Netzwerk an einem
Datensatz der Henon-Zeitreihe trainieren und das Netz
anschließend für eine Vorhersage benutzen. Sie können
dazu das Netz des vorigen Beispiels wieder verwenden.
Fügen Sie Timeser1/Shift
Time ein und verbinden Sie den
Input mit der generierten 1-dim Henonzeitreihe. In der
Standarteinstellung des Algorithmus wird die Zeitreihe
einen Zeitschritt nach vorne verschoben.
-
- Pick Overlap
In unser vorigen Untersuchung haben Sie durch den
Timedelay-Algorithmus eine 2-dimensionale Zeitreihe mit
den Daten y[t]=(x[t],x[t-1]) erzeugt. Mit der
zeitverschobenen Zeireihe z=x[i+1] zusammen liegen die
Beispielpaare vor, um ein Netzwerk auf die Abbildung y[t]à z[t]
zu trainieren. Allerdings existiert durch den Zeitversatz
an den Enden der Zeitreihen nicht für jedes t von y[t]
ein z[t] und umgekehrt. Um reguläre Beispielpaare zu
erzeugen müssen mit Timeser1/Pick Overlapp die Zeitreihen an den Enden
"zurechtgeschnitten" werden. Verbinden Sie die
beiden Inputknoten mit den zwei Zeitreihen. An der
Ausgabenseite erhalten Sie die gekürzten Zeitreihen.
-
- Clustering
Als Vorstufe des neuronalen Netzes benötigen Sie das
"Cluster-Set", das mit Neural Net/Clustering erzeugt wird. Dazu muß die Input-Zeitreihe mit
der (gekürzten) 2-dimensionalen Zeitreihe verbunden
werden. Setzen Sie vorher Size=3000 im
Generate-Henon-Algorithmus. In der grafischen Darstellung
des Cluster-Sets erkennen Sie die berechnete Einteilung
des Phasenraumes.
-
- Fit des Radialen-Basis-Funktionen-Systems
Neural
Net\ RFS-Fitting muß eingefügt
und die Cluster-Sets miteinander verbunden werden. Die
Input-Zeitreihe als Ziel des Fits wird mit der
(gekürzten) 1-dimensionalen Henon-Zeitreihe verbunden.
In dem Ausgabeknoten der RFS-Fits liegt das RBFS vor, was
einem komplettem neuronalen Netzwerk entspricht.
-
- Anwendung des RBFS
Das Netzwerk wird jetzt mit Network/RFS-Calculating auf die Argumente, die in der 2-dimensionalen
Zeitreihe vorliegen, angewendet. In einer Grafik sollten
Sie die berechnete und die originale Zeitreihe visuell
vergleichen. Setzen Sie dazu vorher im
TSPlot-Algorithmus: SetxRange=1, xfrom=0 und xto=50. Mit Timeser2/Comparision erhalten Sie den genauen numerischen Vergleich.
-
- Trainings- und Testset
Für eine echte Vorhersage ist die bisherige
Vorgehensweise nicht erlaubt, da das Netzwerk an den
Trainigsdaten getestet wurde. Generieren Sie jetzt eine
3000 Punkte lange Zeitreihe und teilen diese mit Timeser1/Split bei SplitPos=2000 in zwei Teile. Dazu trennen
Sie das Netz hinter dem Timedelay-Algorithmus auf und
fügen den Algorithmus ein. Das Netz wird nun mit dem
vorderen Teil der Zeitreihe (Output-Verbindungslinie
Nummber 1) trainiert und an dem hinteren Teil getestet.
- Variation
Sie können nun verschiede Variationen des Netzes
oder der Daten untersuchen. Sinnvoll ist z.B. in
Timedelay die Dimension zu verändern oder größere
Vorhersageschritte in Shift-Time mit größerer
Beispielzahl einzustellen.
Das grundsätzliche Arbeiten mit dem Programm
ist an Hand dieser Beispiele erklärt. Den vollständigen
Überblick über die implementierten Algorithmen und die
Möglichkeiten von sinnvollen Verknüpfung erhalten Sie beim
Durcharbeiten der Hilfedateien.
- Literaturverzeichnis
[1] Takens, F., (1981), Detecting
strange attractors in turbulence, Lecture
notes in Mathematics, Vol. 898, 366.[2] Fröhlinghaus, T., Weichert, A.,
Ruján, P., (1994), Hierarchical neural
networks for time-series analysis and control,
Network 6 101-116.
[3] Welch, B., (1995), Practical
Programming in Tcl and Tk, Prentice Hall PTR.
[4] Ousterhout, J.K., (1995), Tcl und
Tk (deutsche Übersetzung), Addison-Wesley.
[5] Stroustrup, B., (1991), C++
- Die Programmiersprache, Addison-Wesley.
[6] Lippman, S.B., (1992), C++,
Addison-Wesley.
[7] Laskar, J., Froeschlé, C., Celletti,
A., (1992), The measure of chaos by the
numerical analysis of the fundamental frequencies,
Physica D 56, 253.
[8] Schreiber, T., (1993), Extremely
simple nonlinear noise-reduction method,
Phys. Rev. E 47 2401
[9] Brause, R., (1991), Neuronale Netze,
B. G. Teubner Stuttgart.
[10] Ritter, H., Martinez, T., Schulten,
K., (1990), Neuronale Netze,
Addison-Wesley.
[11] Hecht-Nielsein, R., (1990), Neurocomputing,
Addison-Wesley.
[12] Moddy, J., Darken, C.H., (1989), Fast
learning in networks of locally-tuned processing
units, Neural Computation 1 281-294.
[13] Stokbro, K., Umberger, D.K., Hertz,
J.A., (1990), Exploiting neurons with
localizied receptive fields to learn chaos,
Complex Systems 4 603-22.
[14] Watanabe, S., (1985), Patter
Recognition: Human and Mechanical, New York:
New York, Ch 6.
[15] Rachold, V., Heinrichs, H., Brumsack,
H.-J., (1992), Spinnweben: Natürliche Fänger
atmosphärisch transportierter Feinstäube,
Naturwissenschaften 79 175.
[16] Heinrichs, H., Brumsack, H.-J., (1984),
Emissionen von Stein- und Braunkohlekraftwerken
der Bundesrepublik Deutschland, Fortschr.
Miner. 62 438.
[17] Pauly, D.P., Muck, J., Tsukayama, M.,
Tsukayama I., (1989), The Peruvian upwelling
ecosystem: dynamics and interactions, ICLARM
Comf. Proc 18, 438.
[18] Palomares, M.L., Jarre, A., Sambilay
V., (1989), Documentation of available 5 1/4 '
MSDOS data discs on the Peruvian upwelling
ecosystem, 408 - 416. In D. Pauly, P. Muck,
J. Mendo und I. Tsukayama (Hrsg.), The Peruvian
upwelling ecosystem: dynamics and interactions.
ICLARM Conference Proceedings 18, 438.
[19] Schuster, H.H., (1984), Deterministic
Chaos, Weinheim: Physik Verlag.
[20] Press, W.H., Flannery, B.P. Teukolky,
S.A., Vetterling, W.T., (1990), Numerical
Recipes in C: The Art of Scientific Computing,
Cambridge University Press.
[21] Bürger G., (1996), Expanded
downscaling for generating local weather
scenarios, Clim. Res. 7 111-128.
[22] Bürger G., Weichert A. (1998), Linear
vs. nonlinear techniques in downscaling, To
be published in Clim. Res
[23] Fischer, A.G., Bottjer, D.J., (1991), Orbital
forcing and sedimentary sequences, J. Sed.
Petrol., 61 1063
[24] Torbett, M.V., (1989) Solar system
and galactic influendes on the stability of the
earth, Palaeogeographie, Paleaoclimatology,
Palaeoecology, 75 3.
[25] Rachold, V.E., Dissertation: Geochemie
der Unterkreide Nordwestdeutschlands: Zyeln und
Events, Georg-August-Universität,
Göttingen, 1994.
[26] Laskar, J., Jountel, F., Boudin, F.,
(1993), Orbital precessional, and insolation
quantities for the Earth from -20 Myr to +10 Myr,
Astron. Astrophys. 270 522.
[27]
Farmer, J.D. Sidorowich, J.J., (1987), Predicting
Chaotic Time Series, Phys. Rev. Lett. 59
845-449.
[28]
Bentley, J.L., (1979), Multidimensional binary
search trees in database applications, IEEE
Transactions on software engineering SE-5(4), 333
[29] Salvino. L.W., Cawley.
R.C., Grebogi, Yorge A.J., (1995). Predictability
in time series, Physics Letters A 209 332

